티스토리 뷰
스도쿠 답 만들기
스도쿠 문제를 출제하는 방법은 다음과 같다. 숫자를 섞어서 답을 먼저 만들어야한다.
- 9x9 빈 칸이 있는 판을 준비한다.
- 편의 상 왼쪽 위에서부터 오른쪽으로 그리고 그 다음 줄로, 0번부터 80번이라는 숫자를 부여한다.
- 각 빈 칸에 1에서 9까지의 숫자 후보가 씌여 있는 카드가 무작위로 섞여 쌓아 놓는다.
- 모든 칸은 다른 칸에 영향을 주는 친구 칸들이 있는데, 일단 같은 3x3 속의 나머지 8개, 바깥으로 가로 6개, 세로 6개, 총 20개가 존재한다.
- 판 전체의 상태 (선택한 숫자와 후보 카드 모음)를 그대로 복사하여 저장할 수 있는 스택이 있다고 가정한다.
- 0번 칸의 숫자를 맨 위에 놓인 카드의 숫자로 선택한다. 현재 모든 판의 상태를 그대로 스택에 저장한다.
- 0번 칸의 친구 칸들 중 1번칸부터 조사하여 후보로 놓여 있는 카드 중에서 0 번칸에 선택한 숫자를 제거한다.
- 1번 칸의 숫자를 맨 위에 놓인 카드의 숫자로 선택한다. 현재 모든 판의 상태를 그대로 스택에 저장한다.
- 1번 칸의 친구 칸들 중 2번칸부터 조사하여 후보로 놓여 있는 카드 중에서 1 번칸에 선택한 숫자를 제거한다.
- 2번 칸의 숫자를 맨 위에 놓인 카드의 숫자로 선택한다. 현재 모든 판의 상태를 그대로 스택에 저장한다.
- 2번 칸의 친구 칸들 중 3번칸부터 조사하여 후보로 놓여 있는 카드 중에서 1 번칸에 선택한 숫자를 제거한다.
- 계속 반복하여 80칸에 후보 카드가 한 장 남으면 적당히 섞여 있는 스도쿠의 답을 완성하게 된다.
- 만약, 칸의 숫자를 선택 후 제거하는 과정에서 어떤 칸에서 하나의 후보카드도 남지 않은 상황이 발생하면, 직전 단계로 돌아가서 해당 스택을 복원하고, 다음 후보카드를 그 칸의 숫자로 지정한다. 즉, 첫번째 카드는 이후 게임을 만드는데 쓸 수 없는 카드인 것이다.
- 12로 돌아가 반복한다.
스도쿠 난이도 조절하기
스도쿠의 답을 먼저 만들었으니, 숫자를 지워 빈칸으로 만들어야한다. 경험 상 쉬운 문제는 50%정도가 빈칸 어려운 문제는 70%가 빈칸이다. 난이도 조절은, 임의의 칸을 삭제하고, 자동으로 풀어가는데, 답이 둘이 있으면 칸 삭제를 원복하고 다른 곳을 삭제하는 식으로 한다.
- 무작위로 원하는 만큼의 칸을 선택해 삭제한다.
- 각 칸에 가능한 후보들의 카드를 찾아 쌓아 놓는다.
- 후보 수가 제일 적고, 번호가 제일 작은 번호의 칸을 답하는 칸이라고 하자.
- 답하는 칸 맨 위에 놓인 카드의 숫자를 선택한다.
- 현재 판의 상태를 그대로 스택에 저장한다.
- 답하는 칸의 친구 칸들을 돌면서 후보 카드 중의 해당 숫자를 삭제한다.
- 3을 가서 반복하여 모든 칸을 채운다.
- 끝까지 채우면 답이 하나 나온 것이다.
- 중간에 친구 칸의 카드를 삭제하는데 후보가 모두 사라지는 상황이 발생하면, 직전으로 돌아가 스택을 복원하여 다음 카드를 선택한다.
- 끝까지 채워도 직전으로 돌아가 스택을 복원하여 다음 카드를 선택한다.
- 끝까지 채우는 경우의 수가 한 번인지를 확인하고, 그런 경우에만 스도쿠 문제로서 가치가 있다.
- 답은 하나여야 하니까.
스도쿠: 답이 여럿인 상황
스도쿠 해를 하나 만들어 본다. 여기에서 출발하여 몇 개를 지워나가면 난이도 조절하여 문제를 만들게 되는 것인데,

일상적이고 평범하다.
스도쿠: 네 칸을 지워 답이 둘
위의 답이 둘인 아주 간단한 경우를 살펴보면 다음과 같다.


노란색으로 칠해진 1,5와 5,1 세로로 된 부분을 살펴보면, 이들 네 칸을 모두 삭제했을 때, 답이 두개가 되는 것을 알 수 있다. 이들은 위 아래로 교환이 가능한데, 일단, 세로와 3x3에서는 변화가 없고, 가로줄에서 변화가 있지만, 맞교환을 하는 것이므로 가로줄에서도 규칙을 깨뜨리지 않게 된다.
이렇게 마주 보고 있는 칸들은 문제를 내기 위해 무작위로 삭제해도 적어도 하나는 남아 있어야한다. 단 네 칸만 지워도 해가 둘이 되는 것이다. 유레카!
스도쿠: 여섯칸을 지워 답이 둘
가로와 세로가 협력하여 교환될 경우 답이 둘이 되는 경우가 있다. 동일한 문제의 답에서 아래 여섯개를 보면 대각선으로 5, 8이 만나고 있다.


이 여섯칸이 모두 지워지고 다음과 같이 씌여도 답이 된다. 가로, 세로, 3x3 의 모든 조건이 유지된다. 문제를 만들 때 이런 여섯칸은 적어도 하나는 남겨 둬야 답이 하나를 유지하게 된다.
스도쿠: 여덟 칸을 지워 답이 둘
이번엔 같은 답에서 다음 칸들을 주목해 보자


첫번째 예와 조금 다르지만 서로 직교하는 모양이다. 왼쪽위의 7,2와 오른쪽 아래의 4, 8을 바꿀 때, 오른쪽 위의 2, 4, 8, 7도 반시계 방향으로 돌려본다. 그래도 스도쿠 규칙을 만족하는 모양이 된다.
즉, 지금 8개의 칸을 모두 삭제한다면, 두 개의 답이 존재할 수 있게 된다. 정말 아름답지 않은가? 이들 여덟칸은 적어도 하나는 남겨 둬야 한 개의 답을 유지하게 된다.
스도쿠: 열칸을 지워 답이 둘
일단 보자.
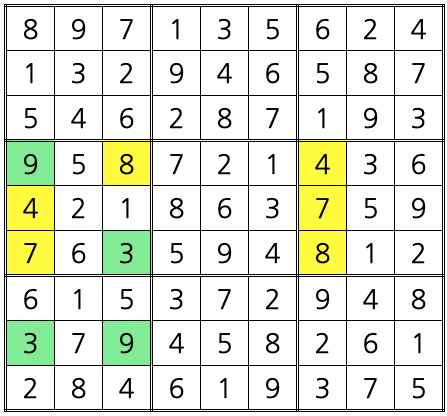

여기서 오른쪽 가운데의 4, 7, 8을 아래로 회전하여 8, 4, 7로 만들고, 왼쪽 아래의 3, 9는 자리를 바꾼다. 그리고, 문제의 중간부분을 시계방향으로 회전한다.
이렇게 총 10개가 참여하여 두 개의 답을 만들어 낸다. 이 10개 중에 하나라도 남아 있다면 답은 하나겠지만, 모두 삭제되면 답이 두 개가 된다.
결론
하나의 답안에도 답이 둘이 되는 경우가 여러 종류로 존재한다. 너무 무작위로만 지우면 안되고, 이런 조건들을 미리 확인하고 지우면 튼튼한 스도쿠 문제를 만들 수 있다.
- Total
- Today
- Yesterday
- url
- VIM
- 벤자민
- SSO
- macosx
- MySQL
- perl
- ssh
- writely
- 수선화
- Linux
- 커피
- 킹벤자민
- nodejs
- 구근
- 디버깅
- tattertools
- 퀴즈
- Tattertools plugin
- BlogAPI
- 식물
- JavaScript
- TCP/IP
- OpenID
- Subversion
- 대화
- SVN
- 덴드롱
- 클레로덴드럼
- 오픈소스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
